在类比系统中研究引力和黑洞的性质
蔡荣根(中国科学院理论物理研究所) 杨润秋(天津大学理学院量子交叉中心)
摘要:引力和量子力学的融合是理解时空起源和引力本质的重要问题,也是一个长期悬而未决的基础物理学根本问题。理论物理学家们对此提出了诸多理论猜想,也做出了许多预言。然而一些相关的预言涉及的效应极其微弱,因此难以通过实验观测加以证实。通过类比引力系统,人们可以将这些引力效应转化为实验室可测可控系统的一些效应。对这些类比系统的研究一方面可以帮助人们更深入地理解引力的性质本身,另一方面也可以为其它相关领域的研究提供启发和新的思路。本文将以几个具体的类比系统为例简要介绍一下类比引力研究的历史和最近的一些研究进展。
正文:
1、前言
广义相对论用优美的几何表述将引力与时空联系在一起。这一理论被提出后一百多年里经受住了无数的实验检验。特别是2016年引力波的直接探测和2019年Event Horizon Telescope(事件视界望远镜) 对黑洞成像进一步验证了广义相对论的正确性。然而这样一个漂亮的理论在理论物理学家的眼中却并不完美。它和物理学中另外一个同样经受住无数实验检验的理论——量子理学——存在着深刻的矛盾。在广义相对论诞生之初,人们就开始寻求它与量子力学的融合。经过数十年不断地探索,人们在这两者的融合上依旧没有找到完美的答案。这其中的原因除了理论本身的困难之外,实验观测上的困难也是其中重要的原因。虽然宏观的引力现象随处可见,但是在微观层面上引力却十分微弱。在目前我们能够实验控制的高能物理过程中,引力效应几乎不起任何作用。在黑洞这样的强引力系统中,人们预期引力的量子效应将扮演者重要的作用。但是从目前的技术能力上来看,人们对于黑洞量子效应的观测依然是遥不可及的。在这样的情形下,人们试图在实验室系统中创造出一个等效的“黑洞”并研究它的相关效应。这一研究被称作“类比引力(analogue gravity)”。它是由著名的 Unruh效应(一个在平坦时空中作加速运动的观测者将看到他处于一个热浴中)的提出者 William Unruh 于1981年首先提出来的[1]。这一研究旨在将弯曲时空中的经典或者量子场的运动规律转化到实验室系统的运动规律中来。经过几十年的发展,目前已经有大量不同的类比系统被相继提出,其中有一些已经在实验上被实现。
在物理学上,人们发现许多不同能标的物理系统会展现出相似的数学规律。这种相似性使得人们可以在研究某一特定的物理现象的时候,用一个相对简单的系统来“类比(analogize)”。这种“类比”在数学和物理的研究中扮演着重要的角色。通过恰当的类比,人们往往可以在不同的物理现象之间建立起桥梁,为一些困难的问题提供新的思路,获得一些意想不到的新发现。特别是,对于物理上一些在极端条件下、难以观测和控制时出现的物理现象,恰当地“类比”可以将它们转化到一些实验室内可以操控的系统中去。通过类比系统来研究引力效应除了可以在技术上实现一些引力系统中暂时无法观测到的现象外,还有许多其它的用处。其中一些模型因为实验原因而有趣,比如在实验技术上实现某些突破或者发展了新的应用等。另一些模型则是因为它们为理解引力之外的其它复杂问题提供了新的思路。在类比引力的研究中,信息流原则上是双向的。有时在广义相对论的范畴内发展起来的洞察力可以用来理解类比模型的某些方面,从而促进我们对类比系统本身物理规律的理解。当然,“类比”不是“等同”。“类比引力”的研究并不能声称其所考虑的类比模型完全等同于引力系统。相反,在这一研究中,人们只是要求类比系统能够捕捉并准确反映广义相对论(有时是狭义相对论)的某些重要特征。
在下文,我们将简要地介绍一下几个具有代表性的类比系统。需要强调的是本文并不打算对这一个领域做一个全面的综述,下面的介绍也不足以全面反映这一领域的历史和现状。相反,它仅仅反映作者对这一领域的看法以及比较关注的方面。特别是,本文将介绍一些利用引力全息对偶和量子模拟来研究引力的非经典效应的进展。虽然这方面的研究很少为传统类比引力领域的研究者所关注,但是笔者认为这类研究是对类比引力研究一个很大的发展,对目前引力理论的研究也具有很大价值。类比引力的研究已经深入到现代物理中的许多分支领域。限于本文的篇幅,一些重要的进展和参考文献无法在这里一一介绍。有兴趣对这一领域有更全面了解的读者,我们建议参阅文献[2-5]以及这些文献所参考的原始文献。
2、声学黑洞
在所有类比引力系统中,最早被提出来和研究最多的就是声学黑洞。在上世纪70年代初,人们发现黑洞具有非零的温度并会自发地向外辐射粒子。黑洞的这一自发辐射现象被称作“霍金辐射”,相联系的辐射温度被称作黑洞的“霍金温度”。霍金辐射的发现为理论上研究引力的量子现象打开了一个窗口。对于一个太阳质量的黑洞而言,其霍金温度只有10-7K的量级。这个温度远远低于宇宙微波背景辐射的温度(约3K)。因此,黑洞的霍金辐射虽然在理论上得到了众多的支持,并被绝大多数物理学家所接受,但是却一直尚未在实验观测上被确认。
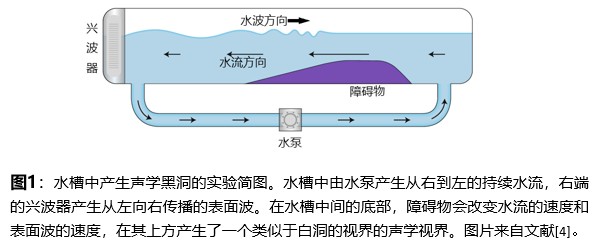
实际上在霍金提出霍金辐射不久,Unruh就注意到一个有意思的“类比”[1]:运动流体中声波的行为类似于引力背景中的标量场的动力学,在声波波速与流体流动的速度等大反向的地方会存在一个与黑洞事件视界相似的分界面。Unruh证明[1]超音速流体流动可以产生一个“哑洞”。这是一个“黑洞”的声学类比,有时也叫“声学黑洞”。流速跨越声速的区域被称作“声学视界”,它是黑洞视界的声学类比。这个类比表明,如果黑洞具有温度并存在霍金辐射的话,这个声学视界也会具有温度并向外自发辐射声子。这一个类比为实验研究黑洞的霍金辐射打开了新的思路。2011年,Unruh和他的同事首次利用如示意图1所示受激辐射实验方案尝试测量声学视界的温度并验证自发辐射是否为热辐射[6]。在实验中,为了形成一个声学视界,实验人员在一个稳定流动的水槽底部设置了一个障碍物。这个障碍物会增加流经其上方的水流流速、同时减小其上方水面的波速。如果恰当地设计水槽和障碍物、并通过水泵适当地控制总水流量,那么在水槽的水面向上游移动的波浪将遇到一个它们无法跨越的点——一个等效的白洞视界。实验人员发现系统存在受激辐射,并且波戈留波夫系数的比值随波长指数递减。利用爱因斯坦受激辐射和自发辐射之间的关系,实验人员得出结论:声学黑洞存在自发的热辐射。不过一些研究人员对这一结果是否足以确认声学视界以及验证霍金辐射仍然有异议。其中一个原因是实验中使用的物理参数并没有在所有相关频率的群速度中产生超临界区域。文献[6]的实验虽然清楚地表明由于流速的变化存在负模转换,但是这种转换似乎来自于两个不同的亚临界区域之间的散射。是否能够将文献[6]获得的指数特征视为霍金辐射存在的证据仍在争论 [7-9]。这个类比实验的第二个缺点在于实验并没有直接验证声学视界的自发声子辐射。在这个经典类比系统中,实验人员必须主动地产生声波去激发视界处的散射。虽然利用爱因斯坦自发辐射和受激辐射的关系可以理论上计算自发辐射的情况,但是这和直接验证类比视界的霍金辐射仍然有一定距离。
Unruh等人对于声学视界研究的另外一个重要的贡献是启发人们逐渐理解了霍金辐射中一个叫做“trans-Planckian”(“跨普朗克”)的重要问题。霍金在黑洞辐射的论证中,霍金辐射被解释成为黑洞吞噬视界附近真空涨落形成的正反粒子对中的反粒子,使得正粒子得以逃脱湮灭的厄运变成真实粒子的现象。由于这些粒子在黑洞视界的外部,因此它们有可能逃向无穷远,形成由黑洞向外辐射的粒子流。这一解释的一个困难之处在于,由于黑洞的引力红移效应,在无穷远处非零能量的辐射粒子,当人们沿着它的轨迹“回溯”时,它的能量会不断地增加。当回溯到黑洞视时,粒子的能量会远远大于普朗克能标。因此,在无穷远处观测得到的能量很低的霍金辐射粒子也是来自由于黑洞附近远高于普朗克能标的粒子。这种高能标的物理涉及到未知的量子引力。这使得人们怀疑霍金辐射会实质性地依赖于未知的量子引力的细节。这在早期构成了对霍金辐射的一个严重挑战[10]。解决这个问题最初的启发并不是来自于引力研究的本身。相反,它却是来自于Unruh对声学黑洞的研究[11]。Unruh 通过声学黑洞的的数值模拟研究,发现黑洞附近高能标的物理并不会影响改变辐射过程,这给黑洞蒸发过程的真实性增加了砝码。在这一工作的启发下,文献[12]较为严格和普适地证明了霍金辐射和黑洞视界附近的高能标物理无关。这个具体事例表明,包括类比引力在内的“类比”研究不仅仅是可以作为“演示实验”将一些困难的物理现象展现在人们的面前,它也是一种帮助人们探索被模拟的系统中未知物理规律的方法。
3、玻色——爱因斯坦凝聚
实际上,像水槽这样的经典物理所主导的模型是无法直接验证霍金辐射的自发辐射性质的。这是因为系统本身的噪声和经典热涨落会远远大于声学视界的霍金辐射。比如在文献[6]采用的如图1所示的实验中,实验人员通过对受激辐射的测量估算出系统霍金辐射的温度大约为10-12K。显然这样低温度的热辐射是无法测量的。为了观察引力的量子性质,我们需要一个真正的量子类比系统。
在目前所研究的量子系统中,玻色——爱因斯坦凝聚体(BEC)是最成功的系统。BEC 在制造声学黑洞方面有许多优势。它不仅可以将温度冷却到10-12K甚至更低,而且描述 BEC 的含时 Gross-Pitaevskii方程可以被改写成一组流体力学方程。另外,BEC 中的声波在波长大于一个被称之为 healing length(愈合长度)的特征尺度时,其波速近似与波长无关。2010 年,Jeff Steinhauer等人[13]提出了一个在 BEC中实现声学黑洞的方案。在他们的方案中,大约10万个铷—87原子通过激光冷却到接近绝对零度形成 BEC 态。同时,他们为BEC流体设计了一个台阶状减小的势能从而能将流体加速到超过BEC中的声速。这样他们在 BEC中创造了一个声学视界。利用这个模型,Jeff Steinhauer 等人在文献[13]提出如何测量并验证霍金辐射的路线图。不过在他们的文章中,他们只是做了数值模拟来证明这样的实验设计可以被用来验证声学黑洞的霍金辐射。
2016年,Jeff Steinhauer 领导的小组首次实现了在BEC中对声学视界霍金辐射的观测[14]。这一实验的关键之处除了需要从技术实现文献[13]所设计的BEC系统之外,还有就是它们采用测量声学视界两侧的“密度—密度”关联函数来探测霍金辐射。这一个方法是由意大利博洛尼亚大学的 Roberto Balbinot和他的同事们在2008年的一篇文章[15]中提出来的。在霍金辐射的物理图像中,霍金辐射是由于黑洞吞噬了真空涨落导致的正反粒子对中的反粒子而形成的。根据量子力学,这种真空涨落的粒子对必定是一对纠缠粒子。这对于任何服从线性方程的场(例如 BEC 中的声波和天体物理黑洞周围的物质场)都是成立的。因此,每一个霍金辐射粒子必定和视界内的另外一个反粒子处于纠缠态。文献[15]指出测量视界两侧密度波动的相关性可以找到霍金辐射存在的证据。经过数千次的重复测量,Jeff Steinhauer获得了他们设计的 BEC系统中声学视界两侧的关联函数。对于短波长(但相比于系统的 healing length 仍然足够长),他们获得正面的测量结果:即声学视界两侧的密度涨落存在由于量子纠缠引起的关联,并发现结果与热辐射一致(尽管实验数据的不确定度还比较大)。图2(a)展示的是 Jeff Steinhauer领导的小组在文献[14]所报道的测量结果。在图2(a)中视界的两侧(绿色环带内)我们可以发现两条模糊但是可以辨识的暗带,这显示了声学视界附近的密度涨落存在量子纠缠。这一实验结果被认为是自发霍金辐射存在的信号。
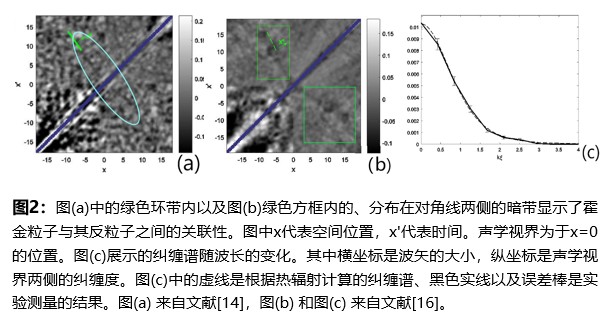
需要指出的是,也有人对 Jeff Steinhauer小组在2016年的实验结果提出了一些质疑。特别是,是否可以将上述BEC中的结果作为类比引力系统中霍金辐射的确凿证据依然还有一些争议,比如见文献[17,18]以及 Jeff Steinhauer本人的回应[19]。在笔者看来,Jeff Steinhauer小组在2016年的结果即便是正确的,也有两个不完美地地方。一方面是实验数据的精度还不够,不确定性还很大,因此所得到结果还没有足够的信服力。另一方面是实验虽然展示存在自发辐射的证据,却无法证明这个自发辐射是一个热辐射,因此也就无法验证声学视界的温度是否和声学视界的霍金温度一致。2019 年 Jeff Steinhauer 领导的小组对他们之前的实验技术进行了重大改进[16]。 图2(b)中展示的是视界两侧声子的密度关联函数,和图2(a)相比,新的结果压低了背景噪声,更加清晰地展示了两侧纠缠粒子的存在。此外,他们在实验中首次测量的声学视界附近自发辐射的声子纠缠谱函数(如图2(b)所示),从而获得了的声子辐射的温度,并发现和声学视界的霍金温度吻合。对于这一实验结果,作者目前还尚未发现有文章对其提出质疑。如果文献[16]的结果被确认是准确无误的话,这将是首次在类比引力系统中直接观测到霍金辐射并测量了相应的温度。
4、光学超材料
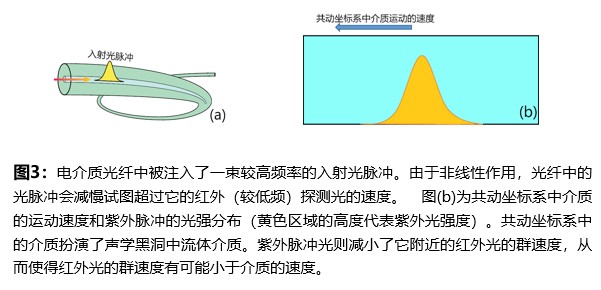
和声学黑洞的原理相似,人们也可以在特殊的光学材料中给光波创造一个“光学视界”。在特殊的光学介质中实现一个等效的视界有多种思路。其中一种常见的思路是和声学黑洞类似。这里只是把声学介质换成光学介质,声波换成电磁波。原则上我们可以将介质的折射率设计得很大,因此可以在局部使得介质运动速度超过介质中的光速,从而为介质中的电磁波提供一个等效的视界。不过在实践中,让介质保持较高的速度运动有一定困难。这里介绍一个由 Leonhardt 在文献[20]中提出的一个非常巧妙的,在静止的介质中实现了一个等效视界的方法。
这一想法可以由图3中的示意图来解释。实验人员在一种非线性的电介质光纤首先注入一段超短脉冲紫外(较高频率)的激光。由于克尔非线性作用,光纤中的光脉冲会减慢试图超过它的红外(较低频)探测光的速度。红外探测光的折射率会随着紫外脉冲光的强度分布不同而不同。文献[20]的一个巧妙之处在于作者将参考系选择为探测光的共动坐标系。由于光纤中的光速实际上是小于真空中的光速,因此选择这样的共动参考系在物理上是允许的。在共动参考系中,入射光脉冲的位置是保持不变的,但是介质却在以相反的速度运动。以紫外脉冲的中心为对称轴,紫外脉冲的强度逐渐减小,因此红外探测光的折射率也逐渐减小。这导致介质中的红外探测光的群速度由紫外光的中心向两侧增大。如图3(b)所示,共动坐标系中的介质扮演了图1中的流体,而紫外脉冲光则扮演了图1中的障碍物,并减小了它附近的红外光的群速度。恰当地设计实验参数就可以为红外探测光制造一个等效的“光学视界”——图1水槽实验中声学视界的“光学版本”。文献[20]在实验中观测到了光学视界附近的红移和蓝移。他们通过理论计算表明这样的系统存在霍金辐射。最近 Leonhardt 在文献[21]报道他们在这个模型尝试对霍金辐射的验证和测量的结果。他们发现了霍金辐射存在的证据,不过实验结果未能获得类似于霍金辐射的黑体能谱。
由于技术的进步,近年来人们可以实现对波导等光学微结构的高精度加工。人工光学材料被用于研究模拟弯曲时空的许多现象。这些人工光学超材料除了被用于研究诸如霍金辐射等涉及弯曲时空中的量子效应外,它们也可以被用于演示广义相对论中一些不容易被观测到的经典效应。比如文献[22]利用微结构光波导来模拟大质量恒星的引力引起的时空弯曲,用来演示引力透镜效应。文献[22]将一个微球嵌入到受控的旋涂过程中形成的平面聚合物波导(图4(b))中。考虑到表面张力效应,微球周围的波导会发生畸变,导致周围波导有效折射率发生连续的变化。在一定条件下,这样的波导可以模拟由强引力场引起的弯曲时空。利用直接荧光成像的方法,文献[22]观察到入射光会渐近地被捕获并聚集在一个不稳定的圆轨道上,如图4(c)所示。这个圆轨道正好对应于一个致密恒星物体的光子球。文献[22]实验方法为广义相对论中描述的引力透镜效应提供了一个有用的类比模型。
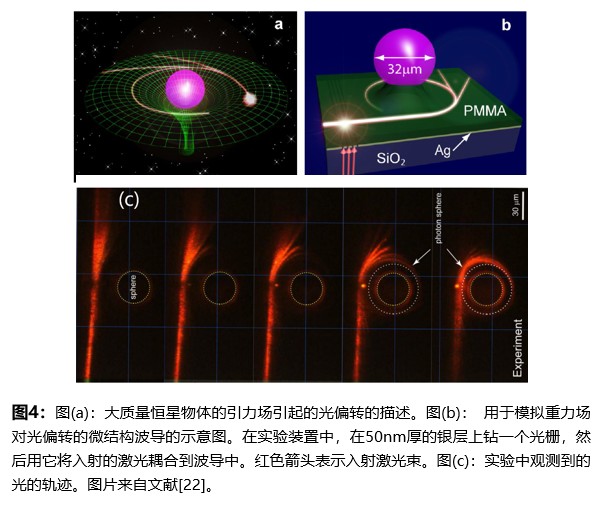
实际上类似的研究不仅可以为描述广义相对论的一些物理现象提供一个可视化的方法,而且可以为人们开发新的光学超材料提供启发。比如前文介绍的文献[22]所提出的微结构波导可以被用作全向吸收体,因此在采光系统和光学微腔系统中具有潜在的应用。再比如文献[23]在广义相对论中的施瓦西解的启发下,提出了一类三维复杂设计的纳米光学结构。在这种结构中光的演化是通过介质的空间曲率来控制的。这种纳米光学结构可以作为弯曲结构中纳米光学的基础,并可用于集成光子电路。
5、类比引力和引力全息对偶
在前文介绍的类比引力研究中,研究者将注意力集中如何在经典或者量子系统/介质中为“声波/光波”或者“声子/光子”构造一个等效弯曲时空背景来实现对弯曲时空量子场论的模拟。其目的在于对黑洞的霍金辐射,引力透镜等弯曲时空中的量子效应或者经典效应进行模拟。经过几十年发展,这一领域已经取得了许多突破性的进展。 然而,最近二十多年引力和黑洞的理论的研究开辟了许多新的方向,带来了许多新的结果。这其中最大的一个进展来自引力的全息对偶性质的发现。
引力的全息对偶原理最早可以追溯到早期对黑洞熵的研究。在上个世纪70年代人们研究黑洞的时候发现黑洞也是一个热力学系统,描述黑洞熵的贝肯斯坦—霍金熵公式表明黑洞的熵正比于黑洞视界的面积[24]。由于物理系统的熵代表着系统的微观自由度,因此贝肯斯坦—霍金熵公式表明黑洞的微观自由度并不是象通常的物理系统那样正比于体积,而是正比于系统的面积。这个重要的特点首先由诺贝尔物理奖获得者‘t Hooft 在1993年注意到[25],并被 Susskind在1994年进一步发展为“引力的全息对偶原理”[26]。最终这一原理经由Maldacena、Steven Gubser、Igor Klebanov、 Alexander Polyakov 和Edward Witten等人进一步发展成为了目前广为研究的“AdS/CFT 对偶”猜想[27-29]。在 AdS/CFT对偶猜想中,一个渐近反德西特时空(一类负常曲率时空)中的量子引力和一个在反德西特时空边界上的强耦合量子场论是等价的。利用引力全息对偶,人们对于引力以及黑洞的“量子”方面有了许多新的认识和预言。这些新的结果和霍金辐射一样揭示了黑洞一些超越经典理论的性质,比如量子混沌、纠缠熵、剪切粘滞比等等。然而目前通过实验室手段来模拟黑洞的这些性质的研究还十分匮乏,实验和理论都还不充分。与经典广义相对论以及诸如霍金辐射等黑洞的量子现象不同,来自引力全息对偶中的许多理论预言还处于探讨阶段。通过类比引力系统的研究有可能为这些理论的研究提供新的启示。
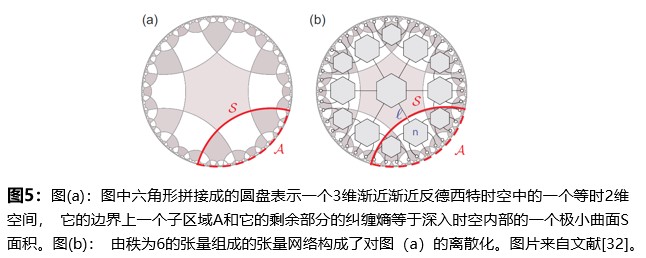
在引力全息对偶中一个非常重要的结论就是渐近反德西特时空中边界上一个子区域的纠缠熵由 Ryu-Takayanagi公式给出[30,31]。根据Ryu-Takayanagi公式,在渐近反德西特时空边界上一个子区域A和它的剩余部分的纠缠熵由深入时空内部的一个极小曲面的面积给出,如图5(a)所示。根据引力全息对偶,连续时空可以被离散化为一个张量网络图表示,如图5(b)所示。能够代表反德西特时空中等时截面的张量网络也被称作“完美张量网络”。利用“完美张量网络”,人们可以获得Ryu-Takayanagi公式的离散版本[33]。文献[32]报道了一个通过模拟全息纠缠熵来模拟量子引力的实验。他们在六位核磁共振量子模拟器上制造出了一个和图5(b) 等价的量子类比系统。在这个量子模型系统中,他们可以通过实验测量得到子区域的纠缠熵来验证 Ryu-Takayanagi 公式。在实验中文献[32]利用时间平均技术来建立6 级的“完美张量网络”,并进行全状态断层扫描来重建实验系统的量子状态。这也是迄今为止核磁共振系统中最大的全态表征。利用数值模拟技术补偿实验中的系统误差后,文献[32]发现实验结果和 Ryu-Takayanagi 公式吻合。这一实验为使用量子类比系统探索引力全息对偶迈出了重要一步,也为在实验室系统中研究量子引力提供了一个实验演示。
实际上从某种意义上讲,引力全息对偶本身就为类比引力的研究提供了广阔的前景。为了理解这一点,我们可以先回顾一下为什么声学黑洞可以作为黑洞的一个类比模型。对于这个问题一个明确的理论回答来自Unruh在文献[11]中的一个结论,即他证明了流体中声波的等效拉氏量都“对偶”于一个弯曲时空(包括黑洞)的标量场理论。正是基于这种“流体/声波”和“弯曲时空/标量场”的对偶关系,人们发展出来了声学黑洞和许多类比引力模型。现在引力全息对偶说的是每一个强耦合的量子场论都“对偶”于一个比它高一个空间维度,渐近反德西特时空中的引力理论。这就告诉我们可以在通过平直时空的强耦合的量子场论来模拟一类特殊引力系统的物理性质。
在这个方面一个有趣的进展来自于文献[34]。根据引力全息对偶,一个量子引力系统和一个量子场论在一定的条件下是等价的。对于后者我们可以将其改写为晶格系统中的量子多体模型,进而在经典甚至量子计算系统中来模拟量子引力效应。在可控量子平台上,文献[34]提出了一个引力全息对偶模型的数字类比模型。这篇文献考虑的是 Sachdev-Ye-Kitaev模型(SYK模型)。该模型描述了相互作用的 Majorana费米子随机地与其它所有的费米子耦合。这个模型在费米子数很大的极限(即所谓的大N极限)和强耦合极限下是一个可解的模型,并且具有共形对称性[35-37];同时它还是一个量子混沌系统,在给定温度下具有最大的李雅普洛夫指数[38]。这些特征强烈地表明,SYK模型具有“近2维反德西特时空”引力理论的全息对偶性质,因而被认为是能够对偶于引力系统的最简单的量子多体模型[37]。因此,如果我们能够对SYK模型进行有效的量子模拟,根据引力全息对偶猜想,这将等效地模拟了一个特殊的量子引力系统。在文献[34]中,作者将SYK模型编码到一个多量子比特系统中,并从理论上展示如何利用量子电路系统和多项式计算资源有效地模拟其动力学。同时他们也指出了如何通过最先进的囚禁离子平台和超导电路来实现他们的理论模型。这为在实验室实现最小量子引力模型铺平了道路,同时也为量子模拟的工具箱添加了新成员。
6、类比引力和量子信息
引力全息对偶的发展也使得引力的研究和另外一个新兴领域——量子信息论——的研究发生了深刻的联系。在以往的众多研究中,研究人员往往将目光聚焦到霍金辐射等典型的弯曲时空量子现象上,对黑洞的“量子信息”方面的物理现象则关注较少。实际上黑洞的量子信息早在霍金辐射的理论被提出之时就已经被人们注意到了。比如贝肯斯坦在1981年提出了“贝肯斯坦熵界”猜想[39-40]:对于给定能量和尺寸的系统来说,黑洞是能储存信息最多的系统。2000年Seth Lloyd在文献[41]提出黑洞是给定能量的情况下最快速的“量子计算机”。最近人们通过引力全息对偶的研究还发现黑洞也是给定温度系统中最为“混沌”的量子混沌系统[38]。这些新的理论研究为类比引力研究提供了许多新契机。与传统的类比引力(各种版本的声学黑洞)不同,为了实现对黑洞量子信息方面的模拟,我们已经知道这样的系统必须具有一些必要的性质。比如,它包含的量子比特数必须与需要模拟的黑洞的熵相同;它应该是一个具有强相互作用的“最为混沌”的系统等。同时,为了能够测量系统的量子信息方面的物理量,这样的系统需要是易于控制,方便测量和理论上干净的系统。
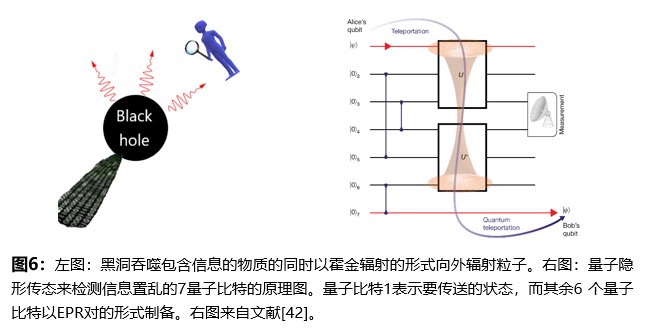
2019年这方面一个有趣的进展来自于文献[42],它与黑洞的信息佯谬有关。长期以来,科学家们一直在思考当物体落入黑洞时会发生什么这个问题,特别是当它是一个量子粒子时。量子物理学的基本规则表明,无论黑洞对量子粒子做了什么操作,它都应该是可逆的。这是由于量子力学中,一个孤立系统的演化必定是幺正的。这一特点保证了孤立系统的信息是守恒的。这一预测似乎与黑洞将物体压成无穷小的点并“喷出”霍金辐射的“嗜好”相悖,因为霍金辐射是不包含信息的热辐射。这个“矛盾”被称作“黑洞的信息佯谬”[43,44]。这是广义相对论和量子力学不相容的一个重要体现。一个成功的量子引力理论必须对这个问题给出一个自洽的回答。引力全息对偶原理的回答是:至少在渐近反德西特时空中,黑洞的演化满足幺正性,因此落入黑洞的信息可以被重构。不过引力全息对偶并没有直接回答落入黑洞的信息是如何“逃逸”出黑洞的。目前已经有多种不同的“逃逸”机制被相继提出。其中一种理论模型认为[45-47]:如果量子信息在黑洞内被迅速“置乱(scrambling)”,那么通过收集黑洞蒸发到原来大小的一半时之前的霍金辐射粒子,我们就有可以恢复出掉入黑洞中的量子信息。十分不幸的是,对于一个恒星质量的黑洞,比如与我们的太阳质量一样大的黑洞,它的质量通过蒸发减小到一半需要1067年——这对于人类来说实在是太长了!因此,人们是无法在真实的黑洞中检验上述观点的正确性。文献[42]在2019年设计了一个“类比”实验来检验这种观点。在实验中文献[42]设计如图6中右图所示的7比特的量子电路用来模拟一个可穿越虫洞。他们的实验表明系统中发生量子置乱越是彻底,则越是能够准确的重构出被传输的信息。他们的实验展示了这样一个事实:由于量子置乱,一个粒子的信息因为被混合或扩散到整个系统中而看起来象是丢失了,但实际上仍然隐藏在不同粒子之间的相互关联中。
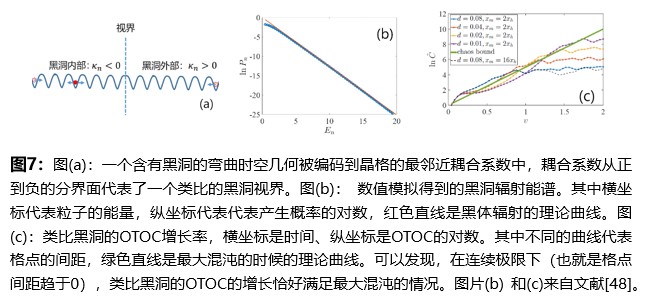
在有关黑洞的研究中,人们经常发现黑洞具有某些极端的性质。引力全息对偶则为黑洞的这些极端性质增加了不少新内容。其中一个就是黑洞是一个最为混沌的量子系统[38]。在描述经典混沌系统时,人们引入了李雅普洛夫指数,它是描述系统对初值的敏感程度的量。一个系统的李雅普洛夫指数越大,表明系统对初值越敏感,因此也就表现的越难以预测。在量子系统中,人们可以通过“非时序关联函数 out-time-order-correlation (OTOC)”来定义一个量子版本的李雅普洛夫指数。一个量子系统的李雅普洛夫指数越大,这个系统就表现的越混沌。文献[38]在一些普适性假设下,根据引力全息对偶证明了在给定温度的量子系统中,黑洞具有最大的李雅普洛夫指数。因此,从这个意义上讲,黑洞是一个最为混沌的量子系统。为了在类比引力系统来研究黑洞的混沌行为,最近在文献[48]中我们提出了一个基于量子多体系统的类比引力模型。这个模型不仅可以实现一些传统的类比引力现象(比如霍金辐射),还可以用来实现验证引力全息对偶的某些结论。文献[48]证明了任意二维静态时空中的无质量标量场总是等价于位置相关的 bosonic hopping 模型,而无质量狄拉克场则等价于与位置相关的 Hubbard 模型或者各向同性XY模型。这个类比模型的关键在于将1+1 维弯曲时空的无质量标量场或者狄拉克场和晶格中紧束缚模型联系起来。弯曲时空的度规则被编码到紧束缚模型中最邻近格点的耦合系数中,如图7(a)所示。作为一个类比引力模型的应用,文献[48]证明了它们可以用来模拟黑洞的霍金辐射,并证明辐射谱满足黑体谱。更为重要的是这个模型可以用来模拟渐近反德西特时空中的黑洞。如图7(c)所示,文献[48]证明了类比黑洞的李雅普洛夫指数确实满足文献文献[38]提出的上界,从而验证了黑洞是自然界中最混沌的系统。
7、结束语
因为黑洞的量子效应极其微弱,所以现在的科技手段还无法探测真实黑洞的这些效应。于是人们一直试图在实验室中寻找一些特殊物理系统,使之可以模拟黑洞的某些量子特性。
利用类比系统研究黑洞,并不苛求面面俱到地展示黑洞的所有性质,而是试图以量子系统的具体数学模型为指导从而捕捉黑洞的部分量子性质。这一研究最初的动力是在实验室系统中试图模拟出霍金辐射等弯曲时空的量子现象。经过多年的发展,人们提出了许多类比引力模型,并且已经在BEC系统中发现了明确的类霍金辐射的实验证据。这些类比引力的研究不仅加深了人们对引力本身的理解,同时也为材料物理、凝聚态物理等实验科学带去新的启发和动力。另一方面,引力理论的研究在近些年也取得了一些新的进展,特别是引力全息对偶的提出以及与量子信息论的结合。这些给类比引力的研究提出了新的挑战,也注入了新鲜血液。更为重要的是,通过对这些类比系统的研究,我们希望能够最终能够回答例如“引力的出现有多普遍?”“当量子修正相当重要时,时空会发生什么?”这样的基本问题[49]。本文以几个模型为例子,简要地介绍以上方面的一些历史背景和进展。类比引力是一个量子场论、广义相对论、流体力学、非线性物理、量子信息和凝聚态物理等领域的交叉课题。这其中任何一个方面的进步都有可能为这个方向的研究带来新的突破。同样,类比引力的研究也会对上述相关领域带来促进作用。相信这一研究会在将来不断地给我们带来新的惊喜。
参考文献:
[1] W. G. Unruh, Experimental black-hole evaporation?, Phys. Rev. Lett. 46 (May, 1981) 1351–1353.
[2] C. Barcelo, S. Liberati and M. Visser, Analogue gravity, Living Rev. Rel. 8 (2005) 12, [gr-qc/0505065].
[3] D. Faccio, F. Belgiorno, S. Cacciatori, V. Gorini, S. Liberati and U. Moschella, Analogue Gravity Phenomenology. Springer International Publishing, Switzerland, 08, 2013.
[4] C. Barceló, Analogue black-hole horizons, Nature Physics 15 (Dec., 2018) 210–213.
[5] M. J. Jacquet, S. Weinfurtner and F. Koenig, The next generation of analogue gravity experiments, 5, 2020. [arXiv:2005.04027].
[6] S. Weinfurtner, E. W. Tedford, M. C. Penrice, W. G. Unruh and G. A. Lawrence, Measurement of stimulated Hawking emission in an analogue system, Phys. Rev. Lett. 106 (2011) 021302, [arXiv:1008.1911].
[7] F. Michel and R. Parentani, Probing the thermal character of analogue hawking radiation for shallow water waves?, Phys. Rev. D 90 (Aug, 2014) 044033.
[8] L.-P. EuvW, F. Michel, R. Parentani and G. Rousseaux, Wave blocking and partial transmission in subcritical flows over an obstacle, Phys. Rev. D 91 (2015) 024020, [arXiv:1409.3830].
[9] A. Coutant and S. Weinfurtner, The imprint of the analogue Hawking effect in subcritical flows, Phys. Rev. D 94 (2016) 064026, [arXiv:1603.02746].
[10] T. Jacobson, Black-hole evaporation and ultrashort distances, Phys. Rev. D 44 (Sep, 1991) 1731–1739.
[11] W. Unruh, Sonic analog of black holes and the effects of high frequencies on black hole evaporation, Phys. Rev. D 51 (1995) 2827–2838, [arXiv:gr-qc/9409008].
[12] R. Brout, S. Massar, R. Parentani and P. Spindel, Hawking radiation without transPlanckian frequencies, Phys. Rev. D 52 (1995) 4559–4568, [arXiv:hep-th/9506121].
[13] O. Lahav, A. Itah, A. Blumkin, C. Gordon, S. Rinott, A. Zayats et al., Realization of a sonic black hole analog in a bose-einstein condensate, Phys. Rev. Lett. 105 (Dec, 2010) 240401.
[14] J. Steinhauer, Observation of quantum hawking radiation and its entanglement in an analogue black hole, Nature Physics 12 (Aug., 2016) 959–965.
[15] I. Carusotto, S. Fagnocchi, A. Recati, R. Balbinot and A. Fabbri, Numerical observation of Hawking radiation from acoustic black holes in atomic BECs, New J. Phys. 10 (2008) 103001, [arXiv:0803.0507].
[16] J. R. Mu˜ noz de Nova, K. Golubkov, V. I. Kolobov and J. Steinhauer, Observation of thermal Hawking radiation and its temperature in an analogue black hole, Nature 569 (2019) 688–691, [arXiv:1809.00913].
[17] A. Finke, P. Jain and S. Weinfurtner, On the observation of nonclassical excitations in Bose–Einstein condensates, New J. Phys. 18 (2016) 113017, [arXiv:1601.06766].
[18] U. Leonhardt, Questioning the recent observation of quantum Hawking radiation, Annalen Phys. 530 (2018) 1700114, [arXiv:1609.03803].
[19] J. Steinhauer, Response to version 2 of the note concerning the observation of quantum Hawking radiation and its entanglement in an analogue black hole, [arXiv:1609.09017].
[20] T. G. Philbin, C. Kuklewicz, S. Robertson, S. Hill, F. Konig and U. Leonhardt, Fiber-optical analog of the event horizon, Science 319 (Mar., 2008) 1367–1370.
[21] J. Drori, Y. Rosenberg, D. Bermudez, Y. Silberberg and U. Leonhardt, Observation of stimulated hawking radiation in an optical analogue, Phys. Rev. Lett. 122 (Jan, 2019) 010404.
[22] C. Sheng, H. Liu, Y. Wang, S. N. Zhu and D. A. Genov, Trapping light by mimicking gravitational lensing, Nature Photonics 7 (Sept., 2013) 902–906.
[23] R. Bekenstein, Y. Kabessa, Y. Sharabi, O. Tal, N. Engheta, G. Eisenstein et al., Control of light by curved space in nanophotonic structures, Nature Photonics 11 (Sept., 2017) 664–670.
[24] J. D. Bekenstein, Black holes and entropy, Phys. Rev. D 7 (Apr, 1973) 2333–2346.
[25] G. ’t Hooft, Dimensional reduction in quantum gravity, Conf. Proc. C 930308 (1993) 284–296, [arXiv:gr-qc/9310026].
[26] L. Susskind, The World as a hologram, J. Math. Phys. 36 (1995) 6377–6396, [arXiv:hep-th/9409089].
[27] J. M. Maldacena, The Large N limit of superconformal field theories and supergravity, Int. J. Theor. Phys. 38 (1999) 1113–1133, [arXiv:hep-th/9711200].
[28] S. Gubser, I. R. Klebanov and A. M. Polyakov, Gauge theory correlators from noncritical string theory, Phys. Lett. B 428 (1998) 105–114, [arXiv:hep-th/9802109].
[29] E. Witten, Anti-de Sitter space and holography, Adv. Theor. Math. Phys. 2 (1998) 253–291, [arXiv:hep-th/9802150].
[30] S. Ryu and T. Takayanagi, Holographic derivation of entanglement entropy from AdS/CFT, Phys. Rev. Lett. 96 (2006) 181602, [arXiv:hep-th/0603001].
[31] V. E. Hubeny, M. Rangamani and T. Takayanagi, A Covariant holographic entanglement entropy proposal, JHEP 07 (2007) 062, [arXiv:0705.0016].
[32] K. Li, M. Han, D. Qu, Z. Huang, G. Long, Y. Wan et al., Measuring holographic entanglement entropy on a quantum simulator, npj Quantum Information 5 (Apr., 2019) ., [arXiv:1705.00365].
[33] F. Pastawski, B. Yoshida, D. Harlow and J. Preskill, Holographic quantum error-correcting codes: Toy models for the bulk/boundary correspondence, JHEP 06 (2015) 149, [arXiv:1503.06237].
[34] L. Garc´ıa-Álvarez, I. Egusquiza, L. Lamata, A. del Campo, J. Sonner and E. Solano, Digital Quantum Simulation of Minimal AdS/CFT, Phys. Rev. Lett. 119 (2017) 040501, [arXiv:1607.08560].
[35] S. Sachdev, Bekenstein-Hawking Entropy and Strange Metals, Phys. Rev. X 5 (2015) 041025, [arXiv:1506.05111].
[36] I. Danshita, M. Hanada and M. Tezuka, Creating and probing the Sachdev-Ye-Kitaev model with ultracold gases: Towards experimental studies of quantum gravity, PTEP 2017 (2017) 083I01, [arXiv:1606.02454].
[37] J. Maldacena and D. Stanford, Remarks on the Sachdev-Ye-Kitaev model, Phys. Rev. D 94 (2016) 106002, [arXiv:1604.07818].
[38] J. Maldacena, S. H. Shenker and D. Stanford, A bound on chaos, JHEP 08 (2016) 106, [arXiv:1503.01409].
[39] J. D. Bekenstein, Universal upper bound on the entropy-to-energy ratio for bounded systems, Phys. Rev. D 23 (Jan, 1981) 287–298.
[40] D. N. Page, The Bekenstein Bound, [arXiv:1804.10623]
[41] S. Lloyd, Ultimate physical limits to computation, Nature 406 (Aug., 2000) 1047–1054.
[42] K. A. Landsman, C. Figgatt, T. Schuster, N. M. Linke, B. Yoshida, N. Y. Yao et al., Verified quantum information scrambling, Nature 567 (Mar., 2019) 61–65.
[43] D. Marolf, The black hole information problem: past, present, and future, Reports on Progress in Physics 80 (jul, 2017) 092001.
[44] J. Polchinski, The Black Hole Information Problem, in Theoretical Advanced Study Institute in Elementary Particle Physics: New Frontiers in Fields and Strings, pp. 353–397, 2017. [arXiv:1609.04036].
[45] B. Yoshida and A. Kitaev, Efficient decoding for the Hayden-Preskill protocol, [arXiv:1710.03363].
[46] B. Yoshida and N. Y. Yao, Disentangling Scrambling and Decoherence via Quantum Teleportation, Phys. Rev. X 9 (2019) 011006, [arXiv:1803.10772].
[47] B. Swingle, G. Bentsen, M. Schleier-Smith and P. Hayden, Measuring the scrambling of quantum information, Phys. Rev. A 94 (2016) 040302, [arXiv:1602.06271].
[48] R.-Q. Yang, H. Liu, S. Zhu, L. Luo and R.-G. Cai, Simulate Hawking radiation and fastest quantum scrambling of black holes by quantum many-body systems, Phys. Rev. Research. 2 (2020) 023107, [arXiv:1906.01927].
[49] J. Maldacena, Black holes and quantum information, Nature Reviews Physics 2 (Jan., 2020) 123–125.
出版商处的全文链接:Physics, 2020, 49(7): 421-430.